X 2 X 3 6
holyeat
Sep 13, 2025 · 6 min read
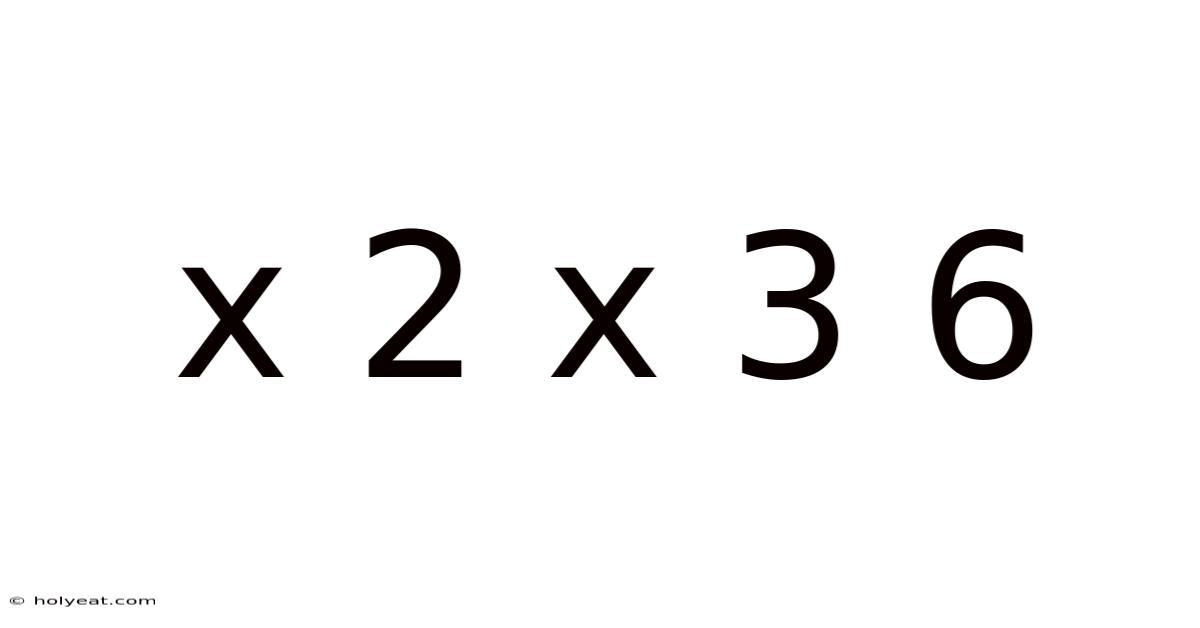
Table of Contents
Unveiling the Magic Behind 2 x 3 = 6: A Deep Dive into Multiplication
The seemingly simple equation, 2 x 3 = 6, acts as a gateway to the vast and fascinating world of mathematics. While children learn this fundamental multiplication fact early on, its implications extend far beyond basic arithmetic. This article delves into the meaning of 2 x 3 = 6, exploring its conceptual foundations, practical applications, and the broader mathematical principles it embodies. We'll unpack the concept of multiplication itself, examine different ways of understanding 2 x 3 = 6, and touch upon its relevance in various fields.
Understanding the Fundamentals: What is Multiplication?
At its core, multiplication is a form of repeated addition. When we say 2 x 3, we are essentially asking: "What is the sum of two 3s?" This can be visualized in several ways:
- Repeated Addition: 3 + 3 = 6. This directly demonstrates the repeated addition aspect of multiplication.
- Arrays: Imagine arranging objects in a grid. Two rows with three objects in each row create a total of six objects. This visual representation makes the concept concrete and easily understandable.
- Groups: Consider two groups, each containing three items. Combining these groups gives a total of six items. This approach helps to grasp the concept of multiplying quantities.
These different methods emphasize that multiplication isn't just an abstract operation; it's a way of efficiently calculating the total when dealing with equal groups or quantities.
Exploring 2 x 3 = 6: Different Perspectives
The seemingly simple equation 2 x 3 = 6 can be approached from several perspectives, each enriching our understanding of its underlying principles:
-
The Commutative Property: Multiplication possesses the commutative property, meaning the order of the numbers doesn't affect the result. This means 2 x 3 is the same as 3 x 2, both equaling 6. This property is crucial in simplifying calculations and understanding the flexibility of multiplication. Visualizing this involves switching rows and columns in our array example – the total number of objects remains unchanged.
-
The Associative Property: Although less directly apparent with only two numbers, the associative property becomes significant when dealing with more than two factors. It states that the grouping of numbers during multiplication doesn't affect the outcome. For instance, (2 x 3) x 1 = 2 x (3 x 1) = 6. This emphasizes the consistency of multiplication regardless of how we group the numbers.
-
The Distributive Property: This property links multiplication and addition. It states that multiplying a number by a sum is the same as multiplying the number by each term in the sum and then adding the products. For example, 2 x (1 + 2) = (2 x 1) + (2 x 2) = 6. This property is essential for simplifying algebraic expressions and solving equations.
The Significance of 2 x 3 = 6: Beyond Basic Arithmetic
While seemingly trivial, the equation 2 x 3 = 6 holds significant weight in various contexts:
-
Real-World Applications: This fundamental equation finds countless applications in everyday life. Consider scenarios like buying two items that cost $3 each, calculating the total number of legs on two tables with three legs each, or arranging six tiles in a 2x3 grid. These everyday examples highlight the practical relevance of multiplication in managing our daily lives.
-
Foundation for Advanced Mathematics: Mastering basic multiplication facts like 2 x 3 = 6 forms the bedrock for more advanced mathematical concepts. It is essential for understanding fractions, decimals, algebra, calculus, and numerous other branches of mathematics. Without a solid grasp of fundamental multiplication, progress in higher mathematics becomes significantly challenging.
-
Understanding Patterns and Relationships: The equation 2 x 3 = 6 embodies fundamental patterns and relationships within the number system. It is a building block for understanding number sequences, patterns in multiplication tables, and the relationships between different mathematical operations. Recognizing these patterns fosters critical thinking and problem-solving skills.
-
Programming and Computer Science: Multiplication is a fundamental operation in computer programming and algorithm design. It's used in countless applications, from simple calculations to complex simulations and data processing. Understanding its properties and efficiency is crucial for developing efficient and optimized code.
Expanding the Concept: Exploring Larger Numbers
While 2 x 3 = 6 is a simple example, understanding the underlying principles allows us to extend this concept to larger numbers. Consider:
-
Multiplying by Tens: Multiplying by tens involves understanding place value and the concept of multiplying by powers of 10. For instance, 20 x 30 = 600 involves understanding that 20 is 2 x 10 and 30 is 3 x 10, leading to (2 x 10) x (3 x 10) = 6 x 100 = 600.
-
Multiplying larger numbers: The same principles of repeated addition, arrays, and groups can be applied to larger numbers. Consider 25 x 32. This can be broken down into smaller, manageable parts using the distributive property, enabling us to handle more complex multiplication problems effectively.
-
Advanced Multiplication Techniques: Methods like lattice multiplication or the Vedic method provide alternative approaches to multiplication, enhancing understanding and providing more efficient ways of solving complex multiplication problems. These methods illustrate that there are multiple pathways to arrive at the correct answer, each with its unique advantages and applications.
Frequently Asked Questions (FAQ)
Q: Why is 2 x 3 the same as 3 x 2?
A: This is due to the commutative property of multiplication. The order of the numbers doesn't change the product. This is intuitively clear when visualizing arrays: two rows of three objects is the same as three columns of two objects.
Q: What happens if we multiply by zero?
A: Any number multiplied by zero is always zero (e.g., 2 x 0 = 0, 3 x 0 = 0). This is a fundamental property of multiplication.
Q: What if we multiply by one?
A: Multiplying any number by one results in the same number (e.g., 2 x 1 = 2, 3 x 1 = 3). One acts as a multiplicative identity.
Q: How is multiplication related to division?
A: Multiplication and division are inverse operations. Division essentially asks, "How many times does one number go into another?" For example, 6 ÷ 3 = 2 is the inverse of 2 x 3 = 6.
Q: How can I improve my multiplication skills?
A: Practice is key! Regularly working with multiplication problems, using various methods like flashcards, games, or online resources, helps improve fluency and understanding. Focus on understanding the underlying concepts rather than just memorizing facts.
Conclusion: The Enduring Power of 2 x 3 = 6
The seemingly simple equation, 2 x 3 = 6, is much more than a basic arithmetic fact. It's a foundational element of mathematics, with implications that extend far beyond elementary school. Understanding its underlying principles, its various interpretations, and its numerous applications helps build a solid foundation for mathematical reasoning and problem-solving skills. From everyday applications to advanced mathematical concepts, the power of 2 x 3 = 6 lies not just in its answer but in its ability to unlock a world of mathematical possibilities. By exploring its depths, we gain a deeper appreciation for the elegance and power of mathematics itself. This exploration should serve as a reminder that even the simplest mathematical truths can hold profound significance and lead to a richer understanding of the world around us.
Latest Posts
Latest Posts
-
Thanks For Your Prompt Answer
Sep 13, 2025
-
Time In Panama Right Now
Sep 13, 2025
-
Food That Starts With Ap
Sep 13, 2025
-
Spanked On The Bare Bottom
Sep 13, 2025
-
Standard Of Beauty In Japan
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.