2 2 X 3 3
holyeat
Sep 19, 2025 · 6 min read
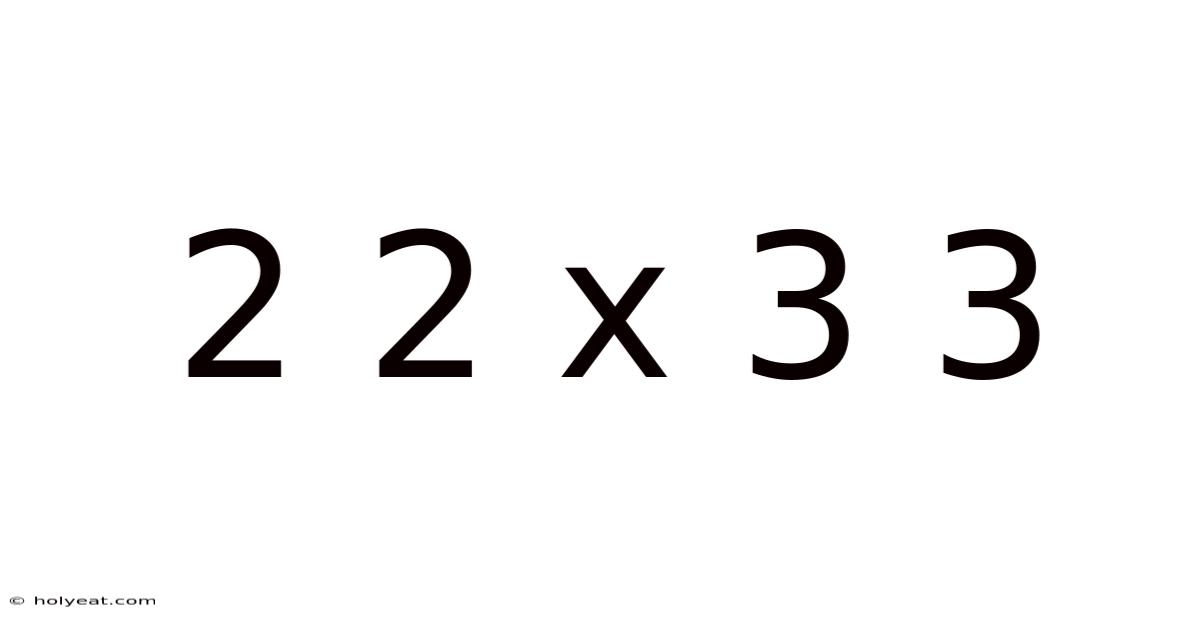
Table of Contents
Decoding 2² x 3³: A Deep Dive into Exponents and Multiplication
Understanding the mathematical expression 2² x 3³ might seem straightforward at first glance, but it opens a door to a deeper understanding of fundamental mathematical concepts like exponents, multiplication, and the order of operations. This article will not only solve the equation but also explore the underlying principles, offering a comprehensive guide suitable for learners of all levels. We'll delve into the intricacies of exponents, explain the reasoning behind the order of operations, and even touch upon the historical context of these mathematical tools.
Introduction: What are Exponents and Why Do They Matter?
Before tackling 2² x 3³, let's establish a firm grasp of exponents. An exponent, also known as a power or index, is a number that indicates how many times a base number is multiplied by itself. In the expression a<sup>b</sup>, 'a' represents the base, and 'b' represents the exponent. So, 2² means 2 multiplied by itself twice (2 x 2), and 3³ means 3 multiplied by itself three times (3 x 3 x 3). Exponents provide a concise way to express repeated multiplication, making complex calculations much simpler and easier to manage. They are fundamental to many areas of mathematics, from algebra and calculus to physics and computer science.
Solving 2² x 3³: A Step-by-Step Approach
Now, let's break down the solution to 2² x 3³ step-by-step:
-
Evaluate the Exponents: The first step is to calculate the value of each term with an exponent.
- 2² = 2 x 2 = 4
- 3³ = 3 x 3 x 3 = 27
-
Perform the Multiplication: Once we have the values of 2² and 3³, we simply multiply them together:
- 4 x 27 = 108
Therefore, the solution to 2² x 3³ is 108.
Beyond the Calculation: Understanding the Underlying Principles
While the calculation itself is straightforward, understanding the principles behind it is crucial for broader mathematical comprehension. Let's explore these principles:
-
Order of Operations (PEMDAS/BODMAS): The order in which we perform mathematical operations is crucial to obtaining the correct result. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) helps us remember the correct sequence. In our equation, exponents come before multiplication, so we calculate the exponents first.
-
The Commutative and Associative Properties: While the order of operations dictates the sequence, it's worth noting the commutative and associative properties of multiplication. The commutative property states that the order of factors doesn't affect the product (a x b = b x a). The associative property states that the grouping of factors doesn't affect the product ((a x b) x c = a x (b x c)). These properties allow for flexibility in how we approach the calculation, although adhering to the order of operations remains vital.
-
Prime Factorization: The numbers 2 and 3 are prime numbers, meaning they are only divisible by 1 and themselves. Understanding prime factorization – the process of expressing a number as a product of its prime factors – provides valuable insight into the structure of numbers. In this case, 108 can be expressed as 2² x 3³. This decomposition is unique to 108, highlighting the fundamental role of prime numbers in number theory.
Expanding the Concept: Working with Larger Exponents and More Complex Expressions
The principles discussed above can be extended to handle more complex expressions involving larger exponents and multiple terms. For example, let's consider 5³ x 2⁴:
-
Evaluate the Exponents:
- 5³ = 5 x 5 x 5 = 125
- 2⁴ = 2 x 2 x 2 x 2 = 16
-
Perform the Multiplication:
- 125 x 16 = 2000
Therefore, 5³ x 2⁴ = 2000. This demonstrates the scalability of the methods we've discussed. Even with larger numbers and higher exponents, the fundamental principles of evaluating exponents first and then performing multiplication remain consistent.
Applications of Exponents and Multiplication in Real-World Scenarios
The concepts of exponents and multiplication are far from abstract mathematical concepts; they have numerous applications in various fields:
-
Compound Interest: In finance, compound interest calculations heavily rely on exponents. The formula for compound interest involves raising a base number (1 + interest rate) to the power of the number of compounding periods.
-
Scientific Notation: Scientists often deal with extremely large or small numbers. Scientific notation, which uses exponents to express numbers concisely, simplifies these calculations.
-
Computer Science: Exponents are fundamental in computer algorithms, particularly in computational complexity analysis, where they help describe the efficiency of algorithms.
-
Physics: Many physical phenomena, like radioactive decay or population growth, are modeled using exponential functions.
-
Geometry: Calculating the volume of cubes or spheres involves exponents; the formula for the volume of a cube, for example, is side³.
Frequently Asked Questions (FAQ)
Q: What if the expression included addition or subtraction?
A: Remember PEMDAS/BODMAS. Exponents are evaluated before addition or subtraction. If the expression had both exponents and addition/subtraction, you would calculate the exponents first, then perform addition and subtraction following the order from left to right. For example, in 2² + 3³ – 4, you would first calculate 2² = 4 and 3³ = 27, then perform 4 + 27 – 4 = 27.
Q: Can exponents be negative or fractional?
A: Yes! Negative exponents represent reciprocals (e.g., 2⁻² = 1/2² = 1/4), while fractional exponents represent roots (e.g., 8^(1/3) = ∛8 = 2). These extensions add significant depth and power to the concept of exponents.
Q: What if the base is a negative number?
A: The rules remain the same. Remember that when raising a negative number to an even power, the result will be positive, while raising a negative number to an odd power results in a negative number. For instance, (-2)² = 4, but (-2)³ = -8.
Q: Are there any shortcuts for calculating large exponents?
A: For very large exponents, logarithmic and computational tools are usually employed. However, understanding the fundamental concept of repeated multiplication is crucial even when using these tools.
Conclusion: Mastering the Fundamentals, Unleashing Potential
This in-depth exploration of 2² x 3³ has not only provided the solution (108) but also illuminated the underlying principles of exponents, multiplication, and the order of operations. These are fundamental concepts that form the bedrock of higher-level mathematics and have wide-ranging applications across numerous disciplines. Mastering these principles provides a strong foundation for tackling increasingly complex mathematical problems and opens doors to further exploration in various scientific and technical fields. By grasping the "why" behind the calculations, we not only solve equations but also develop critical thinking skills that extend far beyond the realm of mathematics. Remember, the journey of mathematical understanding is a continuous process of exploration and discovery.
Latest Posts
Latest Posts
-
Jackson Pollock Free Form Value
Sep 19, 2025
-
Let Me Know Your Thoughts
Sep 19, 2025
-
Guru Gobind Singh Ji Eagle
Sep 19, 2025
-
9 11 Jumper Holding Skirt
Sep 19, 2025
-
Meaning Of Tharki In English
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 2 X 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.