1 X 1 0 X
holyeat
Sep 14, 2025 · 6 min read
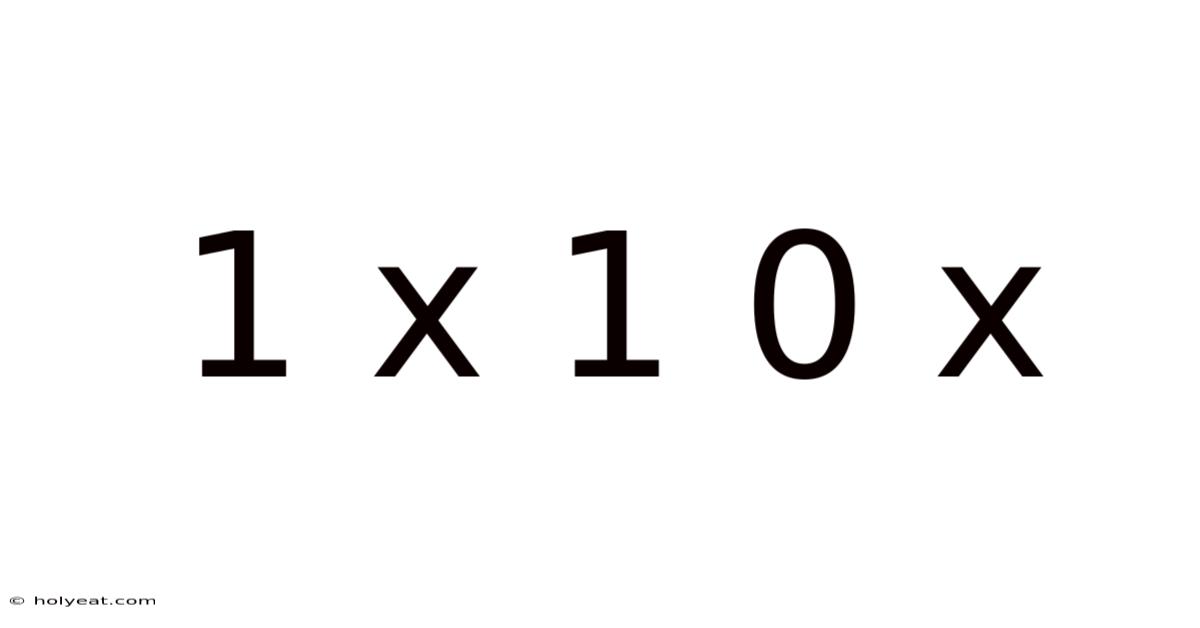
Table of Contents
Decoding the Mystery: A Deep Dive into 1 x 1 = 0 x
The seemingly simple equation, 1 x 1 = 0 x, initially presents a paradox. It appears to contradict fundamental mathematical principles. However, understanding this equation requires delving into the nuances of mathematical notation, the concept of indeterminate forms, and exploring the broader context within which such an expression might arise. This article will unravel this apparent contradiction, providing a comprehensive explanation accessible to a wide range of readers, from those with basic mathematical knowledge to those seeking a deeper understanding of advanced mathematical concepts.
Introduction: Unveiling the Puzzle
At first glance, the statement "1 x 1 = 0 x" seems nonsensical. Basic arithmetic dictates that 1 multiplied by 1 equals 1, not zero times an unknown variable 'x'. This apparent conflict stems from a misunderstanding of how mathematical notation can represent different scenarios. The key to unlocking the puzzle lies in recognizing that this isn't a standard arithmetic equation but a representation of a situation where the result of a multiplication is zero, potentially leading to multiple solutions for 'x'. We'll explore several mathematical contexts where such an equation might arise and how to interpret its meaning.
Understanding Zero and the Multiplicative Identity
Before we delve into the complexities, let's revisit some fundamental mathematical principles. The number 1 is the multiplicative identity, meaning that any number multiplied by 1 remains unchanged (e.g., 5 x 1 = 5). Zero, on the other hand, is unique in that any number multiplied by zero equals zero (e.g., 5 x 0 = 0). This property of zero is crucial to understanding our equation.
Scenario 1: The Zero Product Property
One common scenario where an equation similar to 1 x 1 = 0 x appears is when dealing with the zero product property. This property states that if the product of two or more factors is zero, then at least one of the factors must be zero. Let's consider a slightly modified equation:
(x - 1)(x - 1) = 0
This equation can be expanded to:
x² - 2x + 1 = 0
Notice that the left side is a perfect square trinomial, which factors back to (x - 1)(x - 1) = 0. Applying the zero product property, we see that the only solution is x = 1. Although this doesn't directly match our initial equation 1 x 1 = 0 x, it illustrates a similar principle: a product equaling zero implies that at least one of the factors must be zero.
Scenario 2: Indeterminate Forms and Limits
The equation 1 x 1 = 0 x can also appear within the context of limits in calculus. Consider the expression:
lim (x→0) (x/x)
If we directly substitute x = 0, we obtain the indeterminate form 0/0. This is undefined. However, for all x ≠ 0, the expression x/x simplifies to 1. Therefore, the limit of x/x as x approaches 0 is 1.
Now, let's consider another similar expression:
lim (x→0) (x² / x)
This expression simplifies to lim (x→0) x, which evaluates to 0. In this scenario, we could indirectly relate this to our initial equation by saying that as x approaches 0, the value of x² approaches 0, much like 0x suggests. However, it's crucial to remember that we're dealing with limits, not a direct algebraic equation.
Scenario 3: Solving for x in a System of Equations
Let's imagine a system of equations where one of the equations simplifies to something akin to 1 x 1 = 0 x. For example:
Equation 1: y = x² - 1 Equation 2: y = 0
Substituting Equation 2 into Equation 1:
0 = x² - 1
This simplifies to:
x² = 1
Solving for x, we get x = 1 or x = -1. While we don’t have the exact form 1 x 1 = 0 x, we see a relationship between a product being zero (or in this case, a difference being zero) and finding potential solutions for x.
Scenario 4: Mathematical Models and Approximations
In certain mathematical models and approximations, particularly in physics and engineering, an expression might arise where a product is effectively zero even if the individual factors aren't explicitly zero. This might involve very small quantities that can be treated as approximately zero for the purpose of simplification. The equation could then be used as an approximation, and the solution for x would be interpreted within the context of the model.
Addressing Potential Misconceptions
It's crucial to dispel some potential misconceptions:
- It is NOT a valid arithmetic equation: In standard arithmetic, 1 x 1 = 1, period. The equation 1 x 1 = 0 x is not a standard arithmetic equation; it’s a symbolic representation that can appear in different contexts.
- 'x' is not necessarily zero: While the zero product property suggests that at least one factor must be zero to achieve a zero product, 'x' itself doesn't have to be exactly zero in all scenarios. The equation might represent a situation where 'x' approaches zero or where other factors contribute to the zero product.
- Context is king: The interpretation of 1 x 1 = 0 x is highly dependent on the mathematical context in which it appears. Without knowing the origin of this equation, it’s impossible to give a definitive solution for x.
Frequently Asked Questions (FAQ)
- Q: Can we solve for x in 1 x 1 = 0 x? A: No, not directly. The equation itself is incomplete and needs further context. It's a symbolic representation of a scenario where a product is zero.
- Q: What are the possible values of x? A: The possible values of x depend entirely on the context. It could have multiple solutions, a single solution (possibly 0 or 1), or even be undefined.
- Q: Is this a trick question? A: It’s not a trick question in the sense of being deliberately misleading. However, it highlights the importance of context and the limitations of simple arithmetic in more advanced mathematical situations.
Conclusion: The Importance of Context and Nuance
The equation 1 x 1 = 0 x, while seemingly contradictory at first, serves as an excellent illustration of the nuanced nature of mathematics. It emphasizes the importance of understanding the underlying mathematical principles, recognizing the potential for different interpretations depending on the context, and the limitations of applying simple rules to complex situations. Rather than viewing it as a riddle to be solved, consider it a gateway to explore more sophisticated mathematical concepts such as limits, indeterminate forms, and the zero product property. By exploring the various scenarios in which such an equation might arise, we gain a deeper appreciation for the power and flexibility of mathematical notation and the importance of precise definition and context in interpreting mathematical expressions.
Latest Posts
Latest Posts
-
Blonde Highlights On Dark Blonde
Sep 14, 2025
-
Map Of Canada In 1867
Sep 14, 2025
-
Hair Shades For Fair Skin
Sep 14, 2025
-
Can Cats Eat Ice Cream
Sep 14, 2025
-
Places Hiring Immediately Near Me
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 0 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.