1 Divided By 3 4
holyeat
Sep 16, 2025 · 6 min read
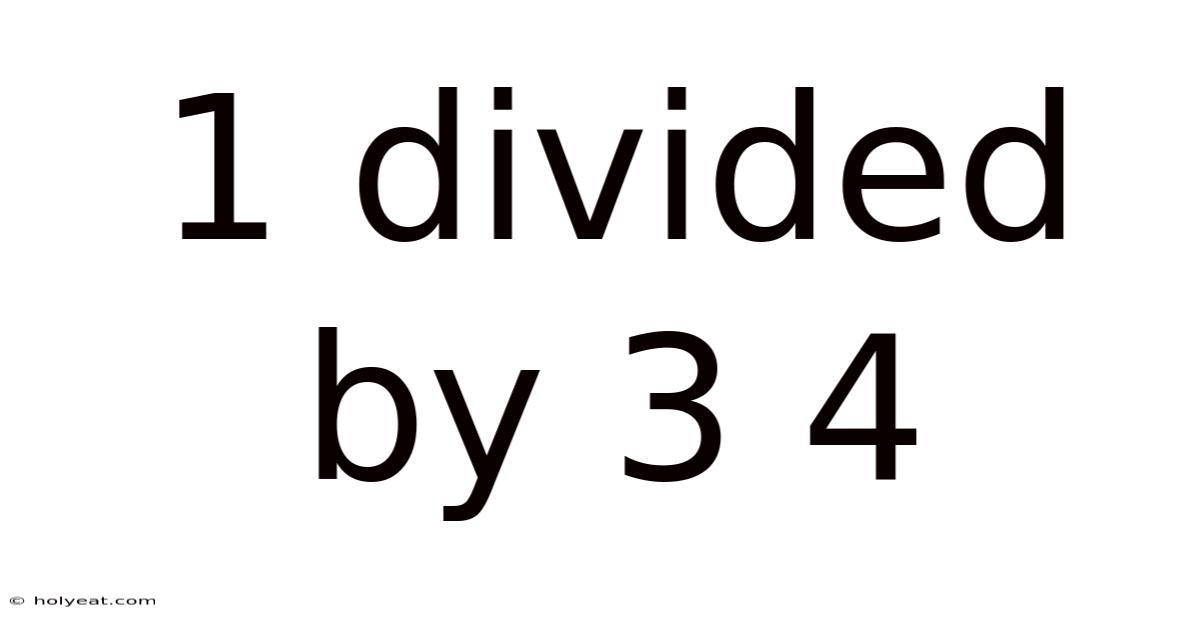
Table of Contents
Unpacking 1 Divided by 3 4: A Deep Dive into Fractions and Decimal Representation
This article explores the seemingly simple calculation of 1 divided by 3 4, delving into the fundamental principles of fractions, decimal representation, and the practical applications of this seemingly basic arithmetic operation. Understanding this concept is crucial for a solid foundation in mathematics and its various applications in everyday life, from cooking and construction to advanced scientific calculations. We will uncover the intricacies behind this calculation, moving beyond a simple answer to provide a comprehensive understanding of the underlying mathematical concepts. We'll cover everything from the basic steps to more advanced considerations, ensuring a clear and thorough explanation.
Understanding the Problem: 1 ÷ (3/4)
Before jumping into the solution, let's clarify the problem statement. We are asked to calculate 1 divided by 3/4, which can be written as: 1 ÷ (3/4). This is a division problem involving fractions. Many find fractions intimidating, but with a systematic approach, the solution becomes clear and straightforward. The key is to remember that dividing by a fraction is the same as multiplying by its reciprocal.
Method 1: The Reciprocal Method
The most straightforward way to solve this problem is by using the reciprocal. The reciprocal of a fraction is simply obtained by flipping the numerator and the denominator. The reciprocal of 3/4 is 4/3. Therefore, our problem transforms from:
1 ÷ (3/4) to 1 × (4/3)
Multiplying 1 by 4/3 is a simple multiplication:
1 × (4/3) = 4/3
Therefore, 1 divided by 3/4 is equal to 4/3. This is an improper fraction because the numerator (4) is larger than the denominator (3).
Method 2: Converting to Decimal Representation
Another approach involves converting the fraction 3/4 to its decimal equivalent before performing the division. To convert 3/4 to a decimal, we simply divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Now our problem becomes:
1 ÷ 0.75
Performing this division using a calculator or long division gives us:
1 ÷ 0.75 = 1.3333...
The result is a repeating decimal, 1.333..., where the digit 3 repeats infinitely. This is represented mathematically as 1.3̅. This decimal representation confirms our previous answer of 4/3, as it is the same value expressed differently.
Converting the Improper Fraction to a Mixed Number
The result 4/3 is an improper fraction. To convert it to a mixed number, we perform a division:
4 ÷ 3 = 1 with a remainder of 1.
This means that 4/3 can be expressed as 1 and 1/3. This signifies that 1 divided by 3/4 equals 1 and 1/3. This mixed number representation offers a more intuitive understanding of the magnitude of the result. It means one whole unit plus one-third of another unit.
Visualizing the Solution
Imagine you have a single whole pizza (represented by the number 1). If you want to divide this pizza into servings of 3/4 of a pizza, how many servings will you have? You can fit one full serving (3/4) into the pizza. Then, you have 1/4 of the pizza left. This 1/4 is 1/3 of the serving size (3/4). Therefore, you have one full serving and one-third of a serving, visually confirming our answer of 1 and 1/3.
The Importance of Understanding Reciprocals
The concept of reciprocals is fundamental to understanding division involving fractions. Remember, dividing by a fraction is equivalent to multiplying by its reciprocal. This rule simplifies complex fraction problems, transforming them into simpler multiplication problems. Mastering the concept of reciprocals is essential for advanced mathematical operations.
Practical Applications
The seemingly simple calculation of 1 divided by 3/4 has numerous practical applications:
-
Cooking: If a recipe calls for 3/4 cup of flour, and you want to double the recipe, you would need to calculate 2 ÷ (3/4) = 8/3 or 2 and 2/3 cups of flour.
-
Construction: If a project requires sections of 3/4 meter long pipes and you have a 1-meter long pipe, you can calculate how many sections you can obtain.
-
Sewing: If a pattern requires fabric pieces of 3/4 yards and you have 1 yard, you can calculate how many pieces you can cut.
-
Finance: Understanding fractions and their decimal equivalents is crucial in calculating interest rates, proportions, and various other financial metrics.
-
Science: In various scientific fields, fractions and their manipulations are fundamental to accurate measurements and calculations.
Frequently Asked Questions (FAQ)
- Q: Why is dividing by a fraction the same as multiplying by its reciprocal?
A: Division is the inverse operation of multiplication. When we divide by a fraction (a/b), we are essentially asking "how many times does (a/b) go into 1?" This is equivalent to asking "what number multiplied by (a/b) equals 1?". The answer is the reciprocal (b/a). Therefore, dividing by (a/b) is the same as multiplying by (b/a).
- Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator. However, understanding the underlying principles is crucial for solving more complex problems and for building a strong mathematical foundation. Calculators are tools, but understanding the 'why' behind the calculation is far more important.
- Q: What if the number being divided wasn't 1?
A: The same principle applies. For example, to calculate 5 divided by 3/4, you would multiply 5 by the reciprocal of 3/4 (which is 4/3): 5 × (4/3) = 20/3 or 6 and 2/3.
- Q: Are there other ways to represent the answer?
A: Yes, the answer can be expressed as a fraction (4/3), a mixed number (1 and 1/3), or a repeating decimal (1.3̅). The best representation depends on the context of the problem.
Conclusion: Beyond the Numbers
This seemingly simple problem, 1 divided by 3/4, offers a gateway to a deeper understanding of fractions, decimals, and the fundamental principles of arithmetic. By exploring different solution methods and considering the practical applications, we move beyond a simple numerical answer to a comprehensive grasp of the underlying mathematical concepts. This understanding is vital not only for academic success but also for navigating the quantitative aspects of everyday life. The ability to confidently manipulate fractions and decimals is a cornerstone of mathematical literacy, empowering you to tackle more complex problems and challenges with ease and confidence. Remember to practice regularly and explore different approaches to solidify your understanding of this important concept.
Latest Posts
Latest Posts
-
Unique Gifts For The Bride
Sep 16, 2025
-
Present Ideas For New Parents
Sep 16, 2025
-
Us Gallons To Imp Gallons
Sep 16, 2025
-
Ltr Per 100km To Mpg
Sep 16, 2025
-
Balkan Yogurt Vs Greek Yogurt
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.